Mathematics of vectors

Imagine if you are given two row vectors a=[a1,a2,a3,.....an] b=[b1,b2,b3,.....bn] Mathematically lets learn some basic operations on vectors

1.Addition

what would a+b result in? a+b=[a1+b1,a2+b2,.....an+bn] (component wise addition ) The first question that springs to mind is, "(Is there something like vector multiplication?)"
Actually there are two types of multiplications supported by vectors.
1.Dot Product
2.Cross Product

Dot Product

If you were given two vectors say a, b then dot product of them is represented by a.b a.b=a1.b1+a2.b2+a3.b3+....an+bn =[row vector of a][column vector of b]

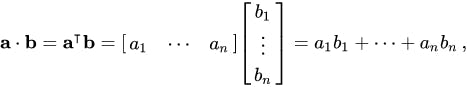
computation of a.b

Geometric perspective of a.b
consider two vectors a(a1,a2) and b(b1,b2) in 2-D space.

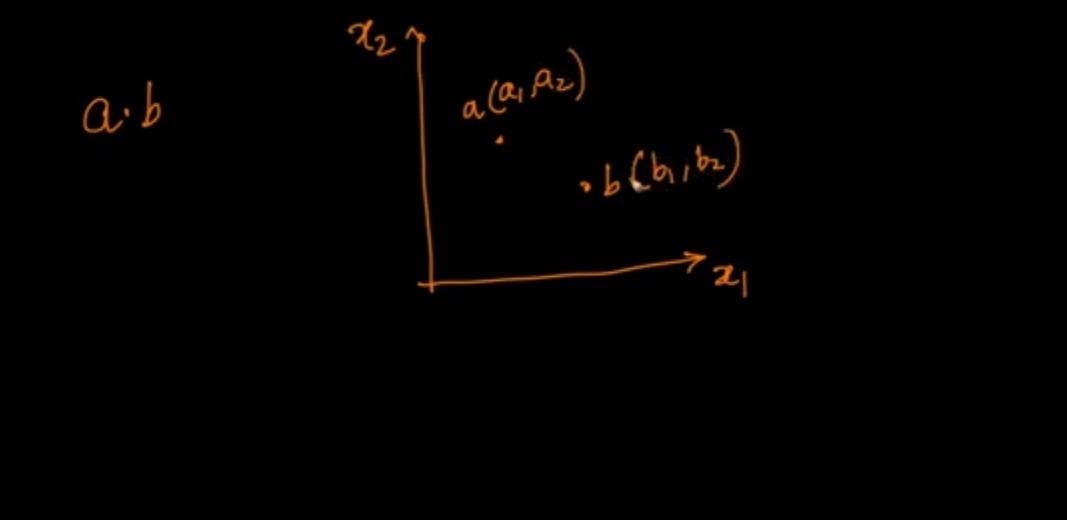
Geometric Interpretation of vectors as a points in space

a.b=||a||.||b||.cosθ

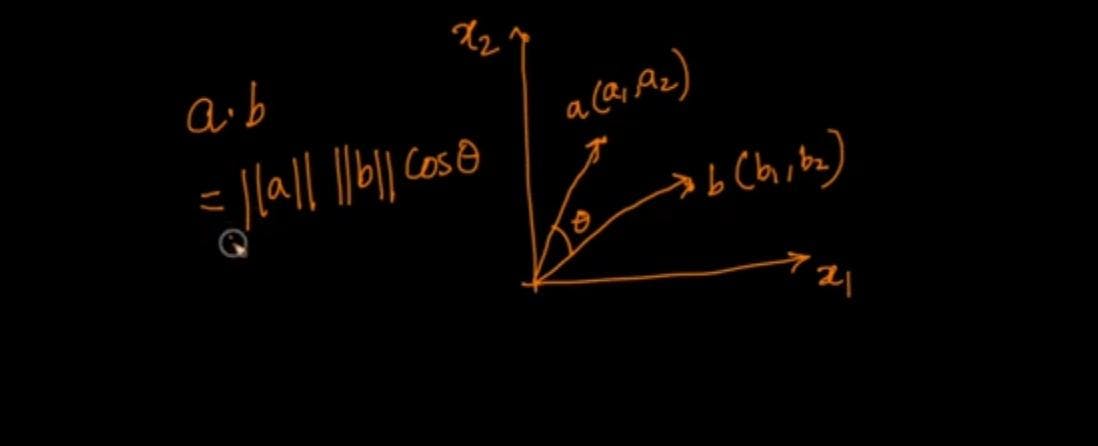
Geometric Interpretation of vectors seperated by an angle

||a||=length of vector 'a' (i.e length of vector 'a' from origin).

How to determine angle between them

a.b=a1.b1+a2.b2 ......(1) similarly, a.b=||a||.||b||.cosθ .......(2) from equation(1) and equation(2) we can conclude that, a1.b1+a2.b2=||a||.||b||.cosθ.
so θ= Cos-1(a1b1+a2b2/||a||.||b||)

special case

let vectors are perpendicular to each other

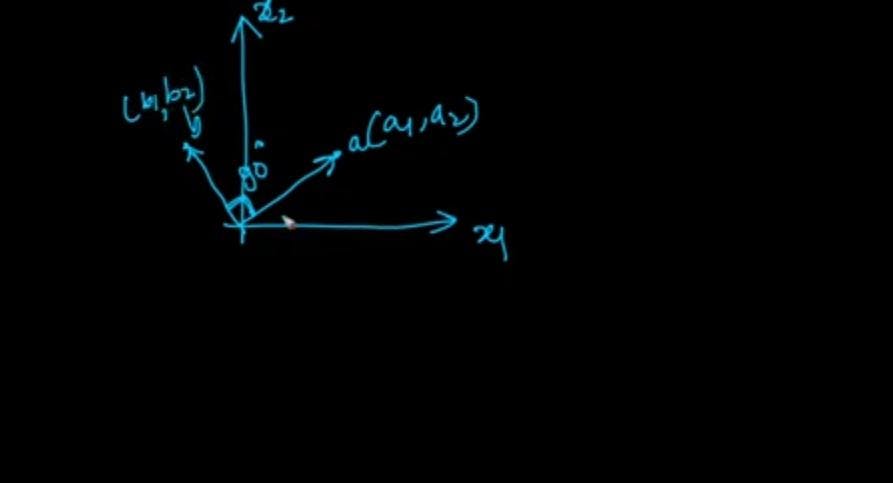a.b=||a||.||b||.cosθ (since perpendicular cosθ=0) a.b=0 we can infer that if cross product of two vectors is 0 then the vectors are perpendicular to each other. This same concept can be extended to N-Dimensional space . a=[a1,a2,a3,.......,an] b=[b1,b2,b3,.....bn] a.b=||a||.||b||.cosθ
𝜃 formula

what about a.a

a.a=a1.a1+a2.a2+a3..a3+.....an.an
=a1^2+a2^2+.....an^2
=||a||^2

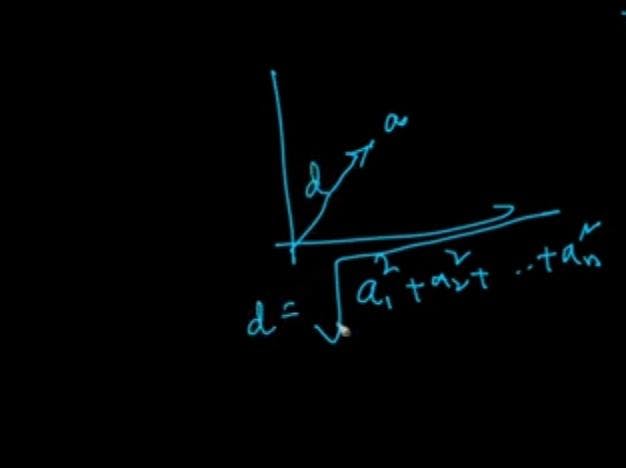
conclusion

The theory just holds good. We have written dot product in 2-D and we have understood it geometrically(as angle between points). We have extended the same idea of dot product to N-D and from that generalization we are understanding geometrical intuition of N-D without actually visualizing it.

Projection

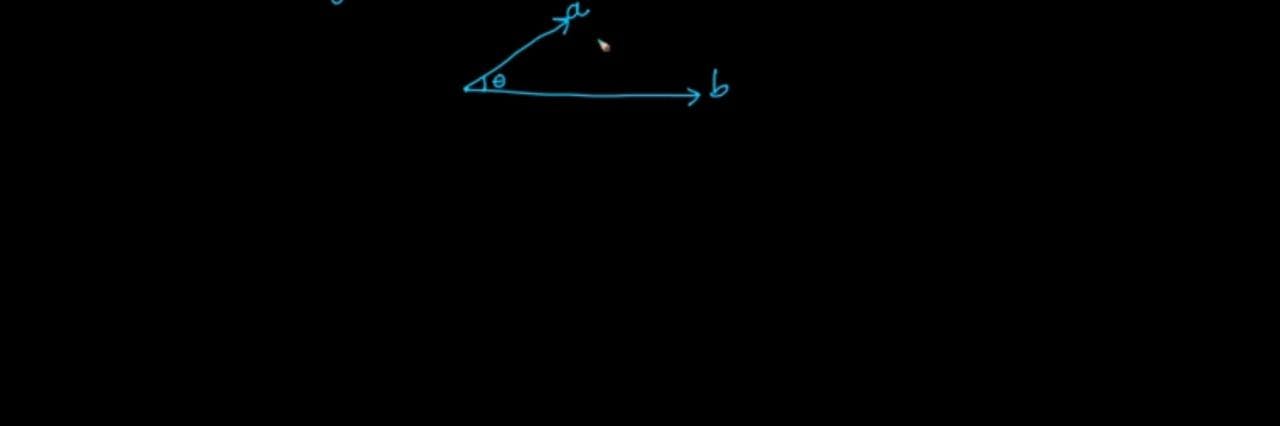Let us suppose we have two vectors a, b separated by angle θ. The projection of vector 'a' onto vector 'b' is take vector 'a' and make it lean perpendicularly on vector 'b'.

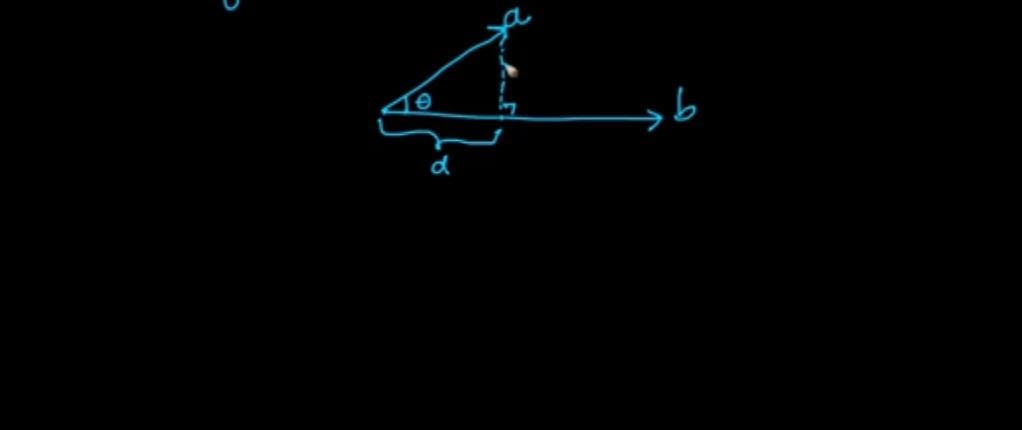d=projection of a on b d=||a|| cosθ -(1) we also know a.b=a1.b1+a2.b2+..... =||a||.||b||cosθ. 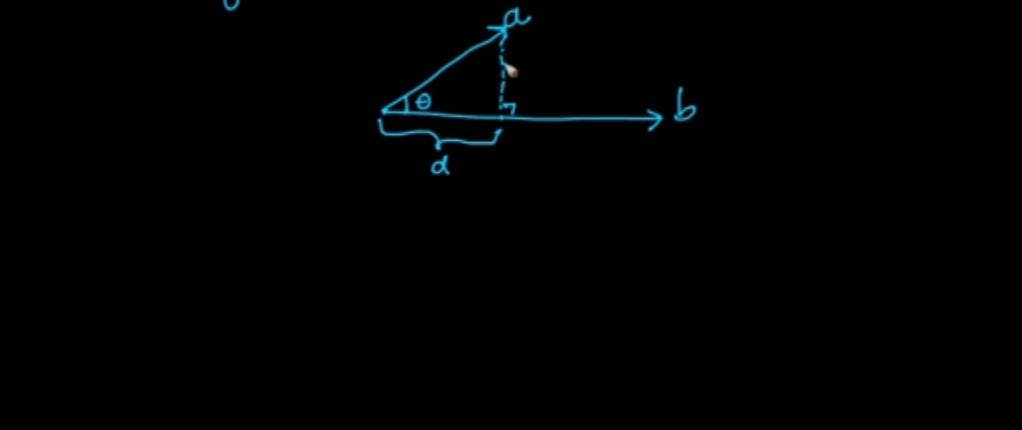so, d=(a.b)/(||b||)
By virtue , if you don't know what θ is and if you just know the components of a & b then you can calculate projection of one vector onto another vector.

Unit Vector

consider a vector a (a1,a2) having two components a1,a2 in a 2-D space. Unit vector is represented by a ^ and a ^ =a/||a||

1. a^ is in same direction as of vector a.

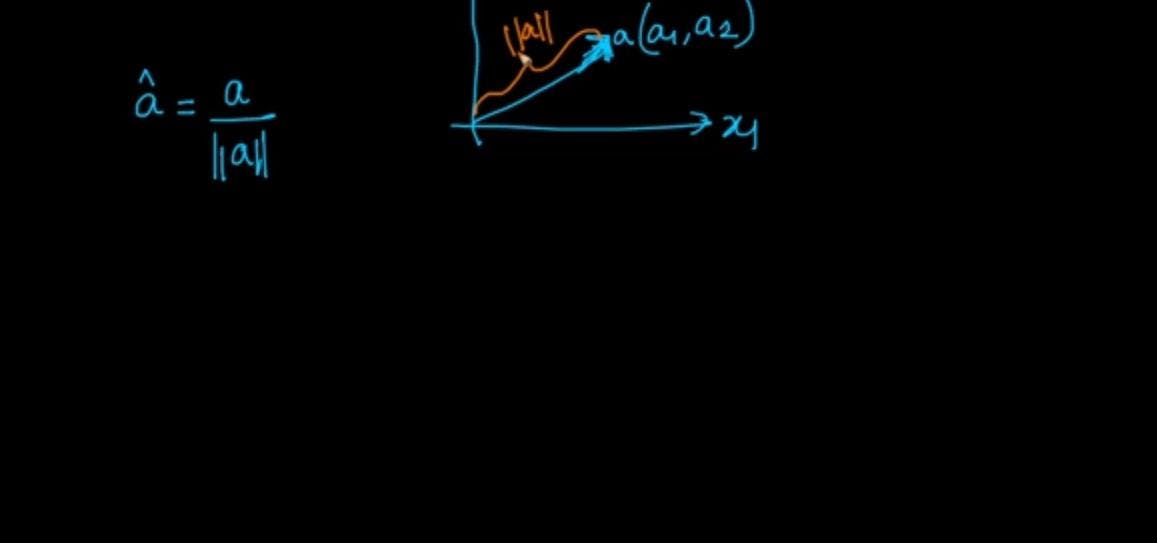
1. || a^||=1 since we are dividing vector a by its length.

LINE

Let us observe how a line looks alike in 2D space. consider two co-ordinate axes x1 and x2.

Geometric representation of Line in 2-D
If you remember from 11th grade math, we wrote the equation of a line as y=m.x+c. ... (1) where 'm' is the slope of the line and 'c' is the y-axis intercept. There is another equation of the line ax+by+c =0 (general form of equation). We can prove both equations are equivalent by just re adjusting equation 2. y =-c/b -(a/b).x where -c/b is c in equation(1) and -(a/b) is m in equation(1) If the axes are x1 and x2, then the line equation is a.x1+b.x2+c=0. can be written as w1.x1 + w2.x2 + w0 = 0. where a = w1, w2 = x2 and c = w0. w1.x1 + w2.x2+w0=0 ......(Line Equation in 2D)

IN 3D space

.

Geometric representation of Line(Plane) in 3-D
The equivalent idea of line in 3D space is plane. and equation of line looks as a.x+b.y+c.z+d=0. this equation of plane can be generalized as w1.x1+w2.x2+w3.x3+w0=0 The plane can separate the 3-D volume into two regions being one above the plane and other being below the plane. The immediate questions that shoots up " What is called in N-D space"? - It is called as Hyperplane. Hyperplane is a generalization concept of line/plane in higher dimensional space.

What is equation of plane in N-D?

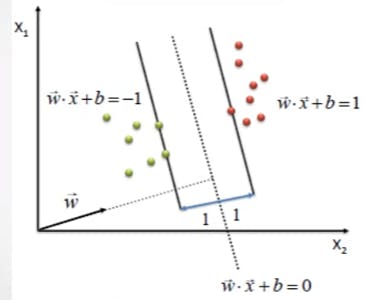
Geometric representation of Hyperplane
In N-D , the equation of plane is w0+ w1.x1+w2.x2+w3.x3+......wn.xn=0 can simply be written as n wo+ ∑ wi.xi =0 (check it). i=1
concise way of writing above equation. using concept of vectors w0+[vector w].[vector x]=0 where vector x is a column vector.
= wo+w^t .x=0 planes are represented with 'Π' (pi) so in any dimension plane can be represented as 'Π'= wo+w^t .x=0

what does w0 exactly convey??

Let us consider 2-D space having a line in it.

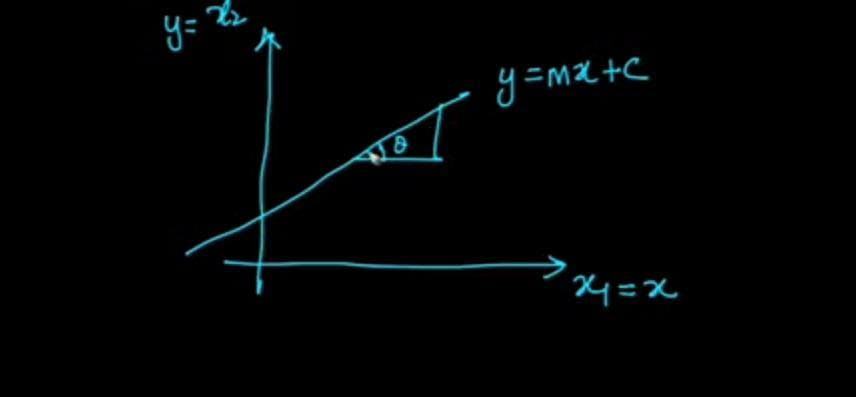
Geometric representation of Line in 2-D

general equation of line is w1.x1+w2.x2+w0=0 . x2=(-w0/w2)+(-w1.x1/w2). where x2= y , (-w0/w2) =c , (-w1/w2)= m and x1=x .

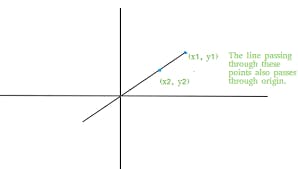
Line passing through origin
If a line is passing through origin then c becomes 0. and we know that c= (-w0/w2) which implies w0=0. line passing through origin. 2-D: w1.x1+w2.x2=0 3-D: w1.x1+w2.x2+w3.x3=0
N-D: w1.x1+w2.x2+w3.x3+.....+wn.xn=0 So simplified equation of line passing through origin can be written as w^t.x=0

Equation of a plane using slightly different geometric Interpretation

consider N-D plane passing through origin. Π=w^t.x=0 and let w be a column vector of N-Dimensions(w1 w2....) and x be a column vector of N-Dimensions (x1,x2.......,xn) . we know that w.x=w^t.x
w.x=||w||. ||x|| cosθ instead of looking w and x as a part of line we have visualized them as vectors. This is the beauty of Linear Algebra, we can just think 'w' as a N-D point so as x. we know that w^t.x=0 so as ||w||. ||x|| cosθ=0 which implies θ=90˚ i.e w and x are perpendicular to each other.

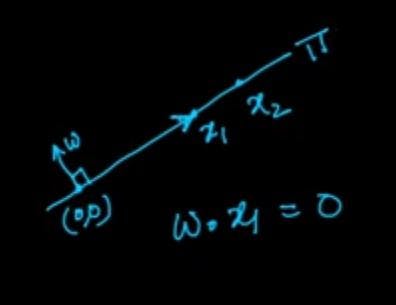
Visualization of vector perpendicular to plane
.

Let us say we have a plane passing through origin and x1 be any point on plane. we know that w is perpendicular to plane at origin(0,0) then w.x1=0 and similarly if x2 is any point on plane then w.x2=0 and can be simplified as if w is perpendicular to plane then w.xi=0 ∀xi ∈ plane..

what does w mean Geometrically

we have just derived w from equation a.x+b.y+c=0. Let us understand what 'w' means. 'W' is a vector perpendicular to plane passing through origin.

w or w^ even then w^.xi=0 ∀xi ∈ plane. For generality we assume our planes pass through origin. In co-ordinate geometry we can shift our axes. Let us say our line doesn't pass through origin then we chan shift our x- axis accordingly to make the line pass through origin.

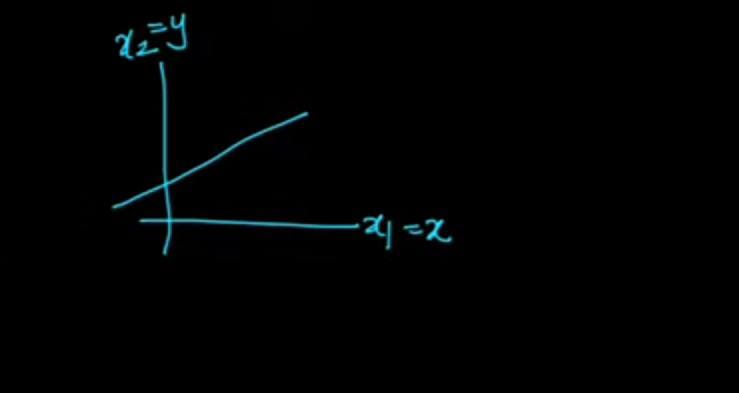
Line not passing through origin
.

.

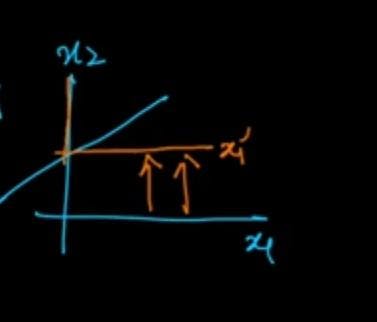shifting the x1-axis upwards in order to make the line pass through the origin
.