Distance of a point from a Plane

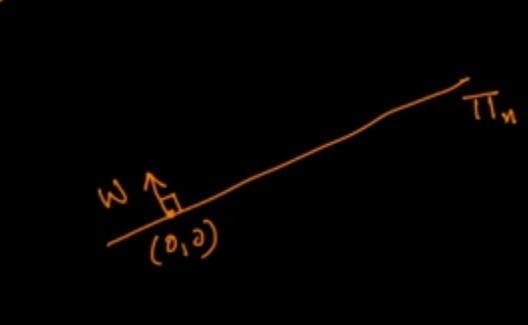Assume that an N-d plane passes through the origin. The plane's equation, w^t.x=0, becomes apparent once you realise that it passes through the origin.

What is the shortest distance of point from plane

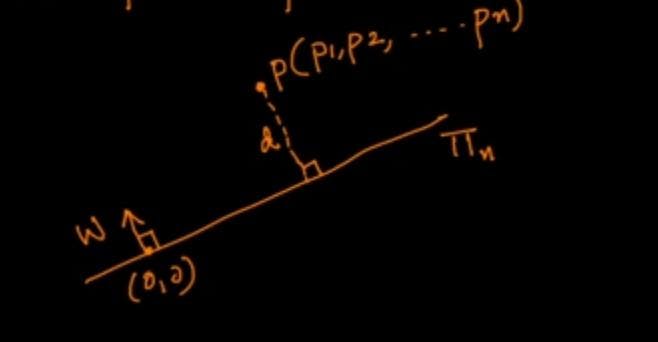
Representation of a point in plane

Imagine if there is a point 'p' having components(p1,p2,.....pn).
Draw a perpendicular from point 'p' onto plane. we can write d as d=w^t.p/ ||w||

proof

.

Computing distance of a point

Let us assume there two points 'p' and 'p1' which are present on either sides of the plane.

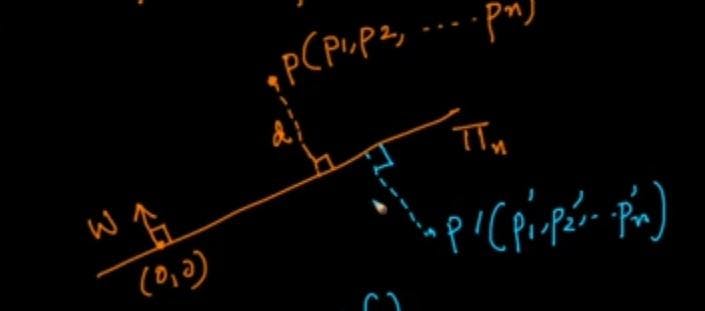d=w.p/ ||w|| if w is a unit vector we can ignore denominator and distance d=w^t.p
if w and p are separated by an angle θ < 90 since w and p are on same side of plane.
A plane in 3-D space separates whole region region in to two spaces, one being above the plane and other being below the plane. These are called as half-spaces .

Representation of half spaces
Lets understand the proof in some detail.

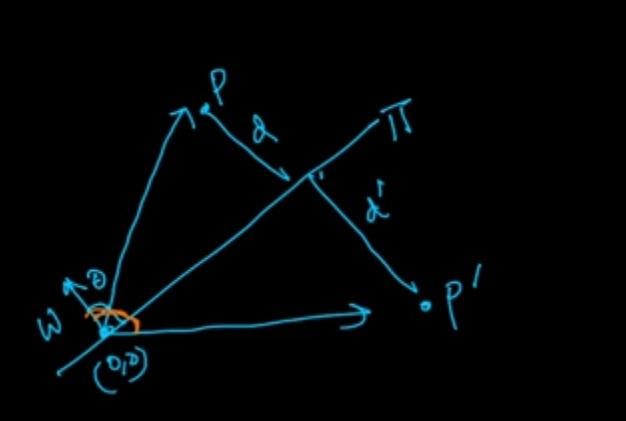
d=w.p/ ||w||
d'=w.p'/ ||w||
since w and p are in the same half space, w.p will be positive and w.p' will be negative. d=w.p/ ||w|| (results in a positive value). d'=w.p'/ ||w|| (results in a negative value). The sign determines to which half space does the point belongs to .

Generalization

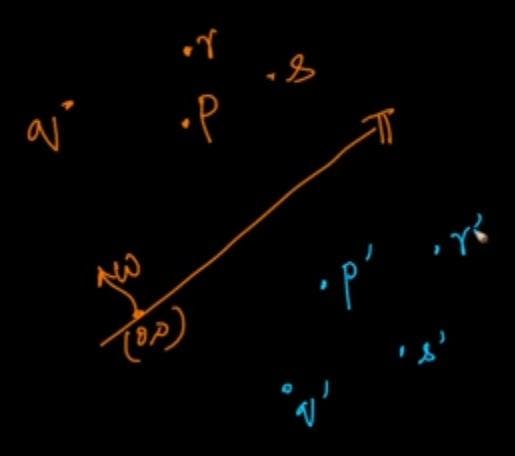
For all points(p,q,r,s) the value w.p/ ||w|| will be positive. For all points(p',q',r',s') the value w.p'/ ||w|| will be negative. If you recall the Iris dataset, you can draw a line such that points which are present above the line belongs to one flower type and which are present below the line belongs to another flower type. This determination can be done using the concept of dot product .

Circle

Let us assume axes (x1 and x2) in 2-D having centre positioned at origin and having an radius 'r'.

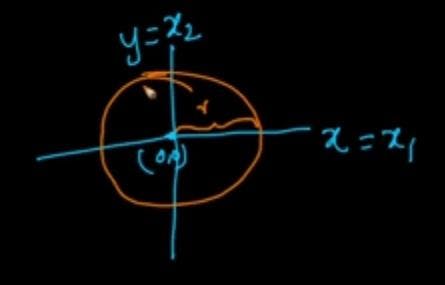
Representation of circle in 2-D having center at origin

The equation of a circle for any point lying on a circle is x² + y² = r²
If the centre lies at some random point, say, (h,k), then the equation of the circle can be modified as, (x - h)² + (y - k)² = r² Just for simplicity, assume the centre of the circle passes through the origin. Let us assume I have a point p(x1,x2) where x1 is the distance from the x1 axis and x2 is the distance from the x2-axis.

How to determine whether point lies inside the circle or outside the circle ?

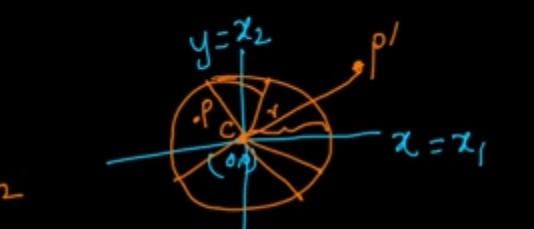
Representation of points lying inside and outside the circle The circle also separates your 2-D space into two parts, one being inside the circle and the other being outside the circle. Given point 'p'(x1,x2)
if (x1)² + (x2)² <= r² then the point 'p' lies inside the circle
if (x1)² + (x2)² > r² then the point 'p' lies outside the circle .
if (x1)² + (x2)² = r² then the point 'p' lies on the circle.
Since we have understood circle in 2-D. Let us extend our learning to higher dimensions.

Circle in 3-D

Suppose we have three dimensions x1, x2,x3 axes. The equivalent of circle in 3-D is sphere.

Representation of circle in 3-D

For any point on a sphere centred at origin, the sphere equation is
(x1)²+(x2)²+(x3)² = r².
In N-D , sphere is equivalent to hypersphere. For any point on a sphere centred at origin, the sphere equation is (x1)²+(x2)²+(x3)²+.........(xn)² = r².
if (x1)² + (x2)²+.....+(xn)² <= r² then the point 'p' lies inside the hypersphere.
if (x1)² + (x2)² +.....+(xn)²> r² then the point 'p' lies outside the hypersphere . if (x1)² + (x2)²+......+(xn)² = r² then the point 'p' lies on the hypersphere.

Ellipse

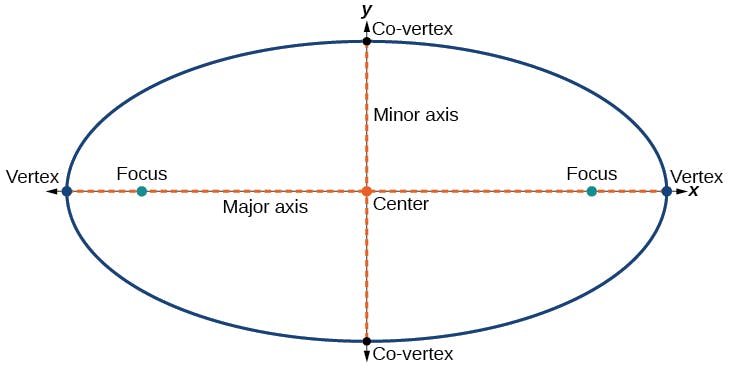
Representation of Ellipse in 2-D

Let us assume axes (x1 and x2) in 2-D having centre positioned at origin and having a minor axes length 'b' where 'b' is length from center to 'y' axis ,and major axes length 'a' where 'a' is length from center to 'x' axis.
In Machine Learning we use planes more extensively where, as usage of ellipse is minimal. The equation of ellipse having center positioned at origin is: 𝑥^2/a^2+𝑦^2/b^2=1

How to determine whether point lies inside the ellipse or outside the ellipse ?

If 𝑥^2/a^2+𝑦^2/b^2 If 𝑥^2/a^2+𝑦^2/b^2>1 'p' lies outside of the ellipse.
If 𝑥^2/a^2+𝑦^2/b^2=1 'p' lies on the ellipse.

IN 3-D

Ellipse in 3-D is called as Ellipsoid.

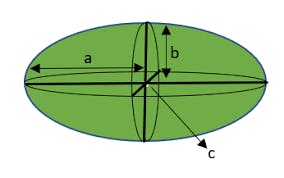
Representation of Ellipse in 3-D

The equation of ellipsoid having center positioned at origin is: 𝑥^2/a^2+𝑦^2/b^2+z^2/c^2= 1.

How to determine whether point lies inside the ellipse or outside the ellipse in 3-D?

If 𝑥^2/a^2+𝑦^2/b^2+z^2/c^2 If 𝑥^2/a^2+𝑦^2/b^2 +z^2/c^2>1 'p' lies outside of the ellipse.
If 𝑥^2/a^2+𝑦^2/b^2 +z^2/c^2=1 'p' lies on the ellipse.

IN N-D.

Ellipse in 3-D is called as Hyper-Ellipsoid.
The equation of ellipsoid having center positioned at origin is: (𝑥1)^2/a^2+𝑦^2/b^2+z^2/c^2+........= 1.

How to determine whether point lies inside the ellipse or outside the ellipse in N-D?

𝑥^2/a^2+𝑦^2/b^2+z^2/c^2 𝑥^2/a^2+𝑦^2/b^2 +z^2/c^2>1 'p' lies outside of the ellipse.
𝑥^2/a^2+𝑦^2/b^2 +z^2/c^2=1 'p' lies on the ellipse.

Squares, Rectangles

consider 2- D space having axes x1 and x2.

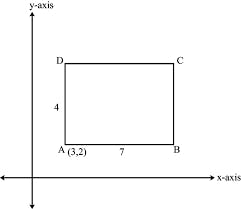
Axes parallel rectangle

consider the rectangle whose points are (2,4),(2,3),(5,3),5,4) as shown.

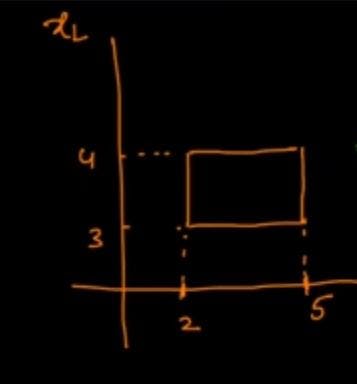
How to determine if point 'p'(p1,p2) lies inside the axes parallel rectangle

if (p1 2) (constraining space on x-axis)
{
if (p2>3 && p2 {
then 'p' lies inside this rectangle.
}
}

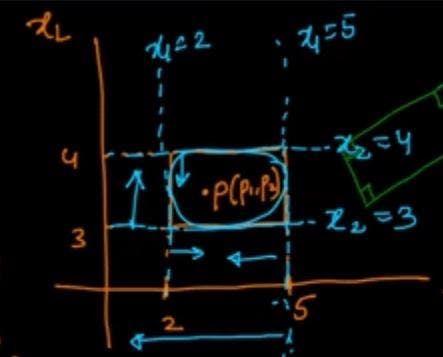
Visualizing the above mentioned conditions.