About Linear Algebra
Linear Algebra is a very fundamental area in mathematics, but we will use it for a wide range of applications. In terms of Machine Learning, it is used to solve specific types of problems. Let me motivate you with a simple example. Assume we have two Iris data set features, f1(petal length) and f2 (petal width), where f1 is along the x-axis and f2 is along the y-axis. We have two types of flowers, one marked with an 'x' and the other with a '0'.
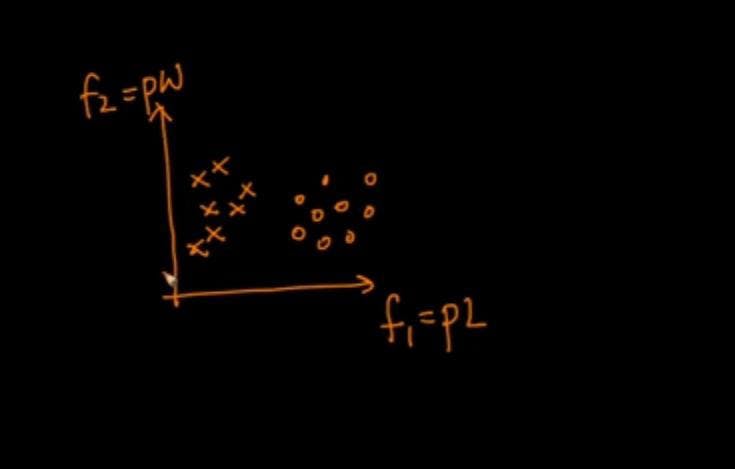
Here 'X' represents petal length, 'Y' represents petal width.
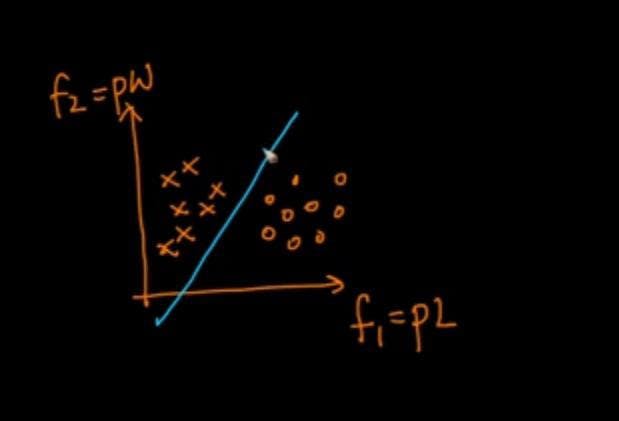
In the above graph, we can see that a line in 2D space distinguishes between Petal length & Petal width.
To distinguish one flower from another, draw a line as depicted above, and we'll notice that flowers on the left side of the line belong to one class, while flowers on the right side of the line belong to another.
If we were to carry out the same task in 3-D, we would indeed require three features, f1, f2, and f3. To distinguish flowers, we must draw a plane as illustrated below.
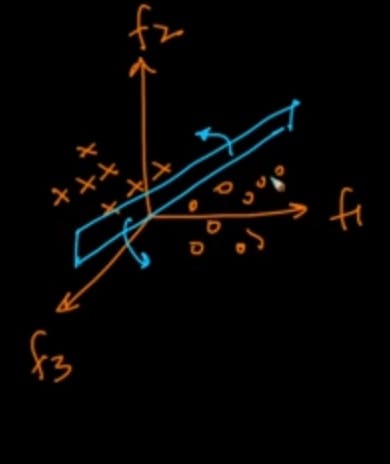
We can see that in 2D, we used a vertical line as an isolation medium, whereas in 3D, we used a plane.
Interceptions about N-Dimensional(4-D.... N-D)?
Linear algebra comes in handy in these scenarios. Linear algebra is a terrific mathematical tool that allows us to stretch our learning and intuition from 2-D and 3-D to higher-dimensional spaces. You'll notice that the lines, planes, and everything else are all coupled together by elegant mathematics. Linear algebra allows us to work in higher-dimensional spaces. If you have 10 features in machine learning, you are operating in 10-D space. conclusion We can't visualize data over 4-D space in such scenarios Linear Algebra becomes handy.
Point (or) Vector
Let us assume we have a co-ordinate axes typical(x-y) axis, just for generality consider co-ordinate axes as x1, x2 [x1= along x-axis, x2=along y-axis]

Above graph represents the typical version of the viewing coordinates axis in 2D space.
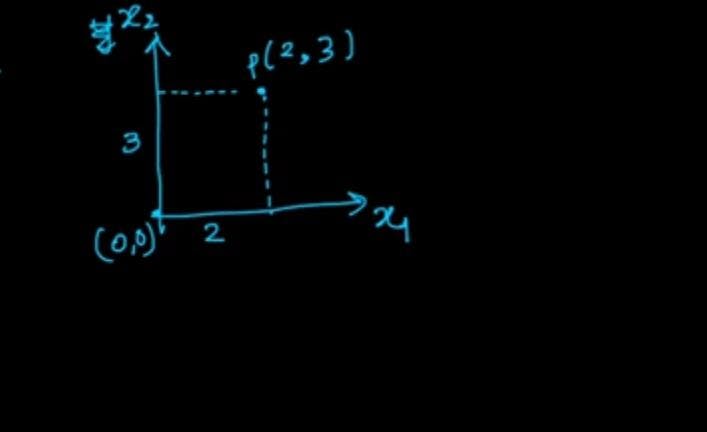
Representation of a point in 2D viewing space.
From the above diagram, you can observe a point in 2D space, and p is represented as p(x1,x2) where x1 is the distance to the point from the origin along the horizontal line. Let it be 2 units x2= distance to point from the origin along the vertical line. Let it be 3 units then p(x1,x2)=(2,3).
we can write point p as a 2-D vector, p=[2,3], where '2' is the x1 component of the vector and '3' is the x2 component of the vector.
Representation of point in 3-D space.
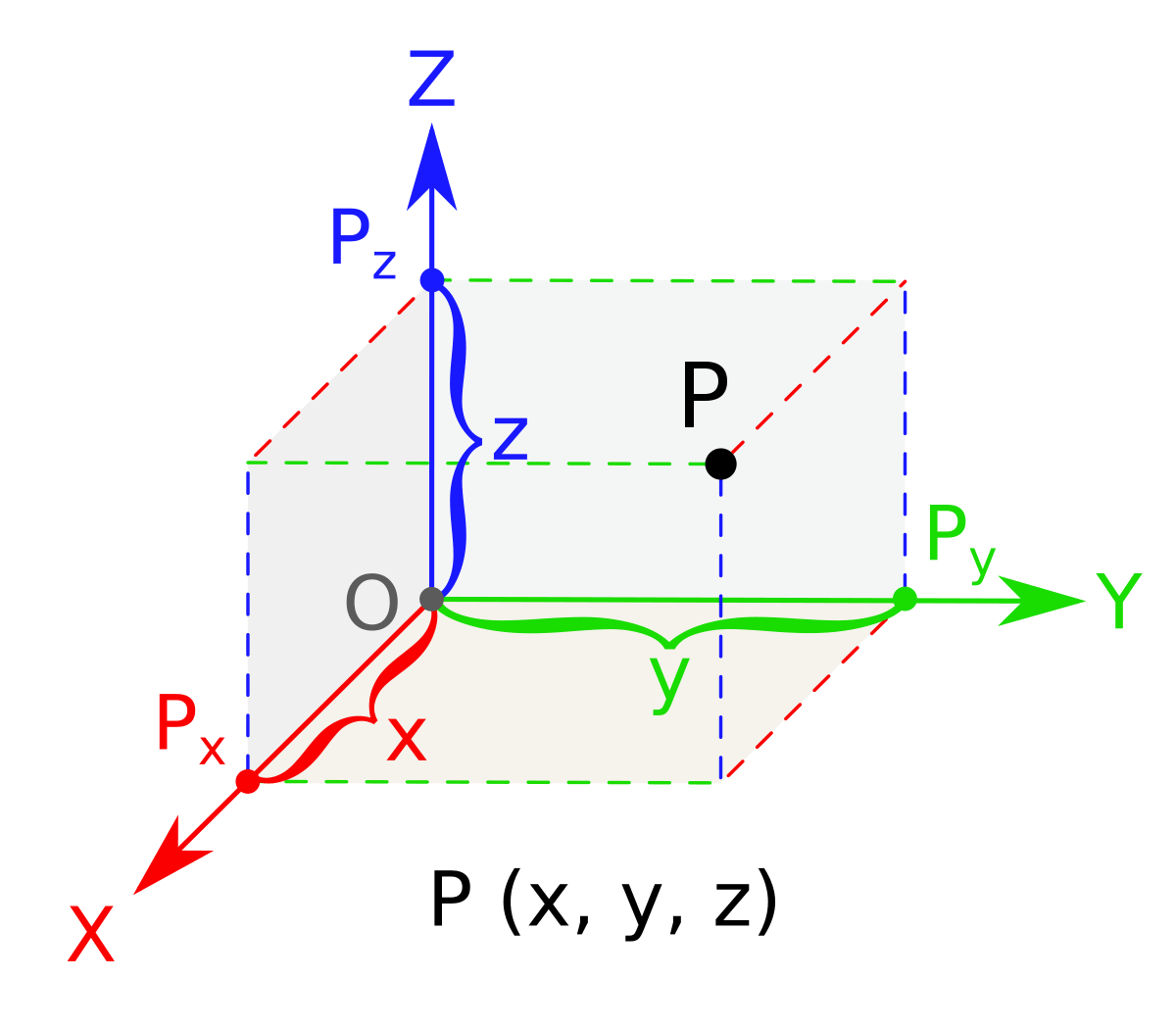
Representation of points Px, Py, Pz in 3D
Represent a point in N-D space.
Let x be a point in N-Dimensional space, then assume a point x=[2,3,4,1,5,......] where these values are components along each axis.
Calculate the distance of the point from the origin.
Consider a 2D - space where p is a point in 2-D space as shown below in the image. p(x1,x2)=(a,b)
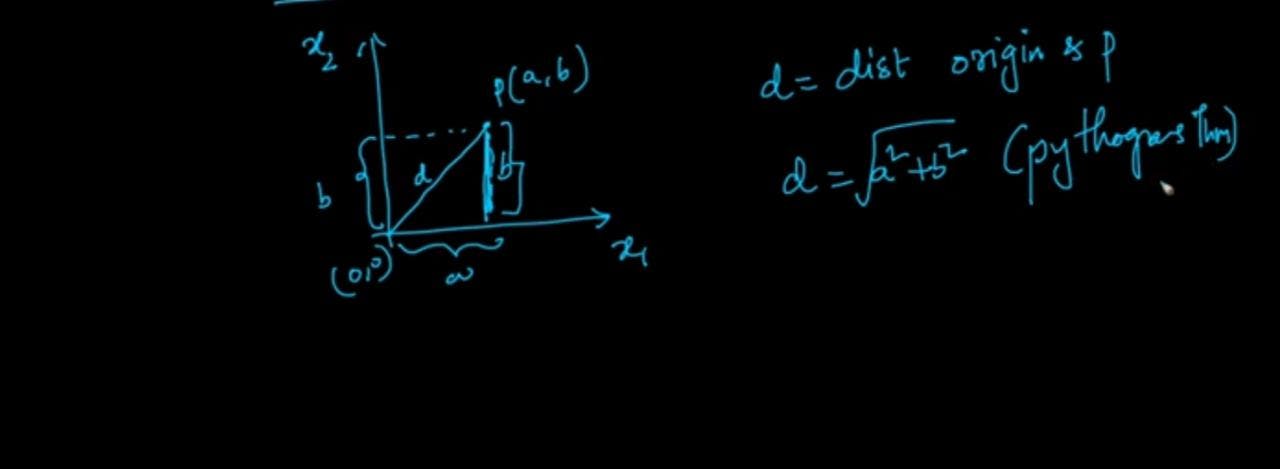
A point p is being represented in 2D space.
Let d be the distance between origin & point. Such that using Pythagoras theorem.
d = sqrt((a^2)+(b^2))
Calculate the distance of the point from the origin in 3D.
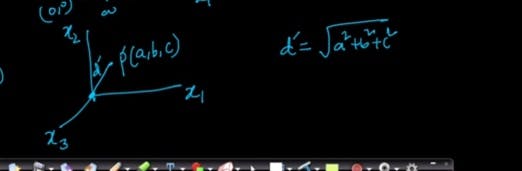
A point p is being represented in 3D space.
Let d' be the distance between origin & point.
d'=sqrt(a^2+b^2+c^2)
What about in N-D?
Let p=[a1,a2,a3,....an] so distance from origin to point in N-D space.
Let d(p) be the distance between the point in N-D to the origin.
d(n) = sqrt(a1^2+a2^2+a3^2+......an^2)
Distance between two points in 2D.

p(x1,x2)=(a1,a2) where a1 is distance between origin to point on x1-axis and a2 is distance between origin and point on y-axis(x2-axis). And similarly, q(x1,x2)=(b1,b2) so the distance between them is represented by
d=sqrt((a1-b1)^2 +(a2-b2)^2)
Proof: construct a right-angled triangle for the above image which turns out to be.
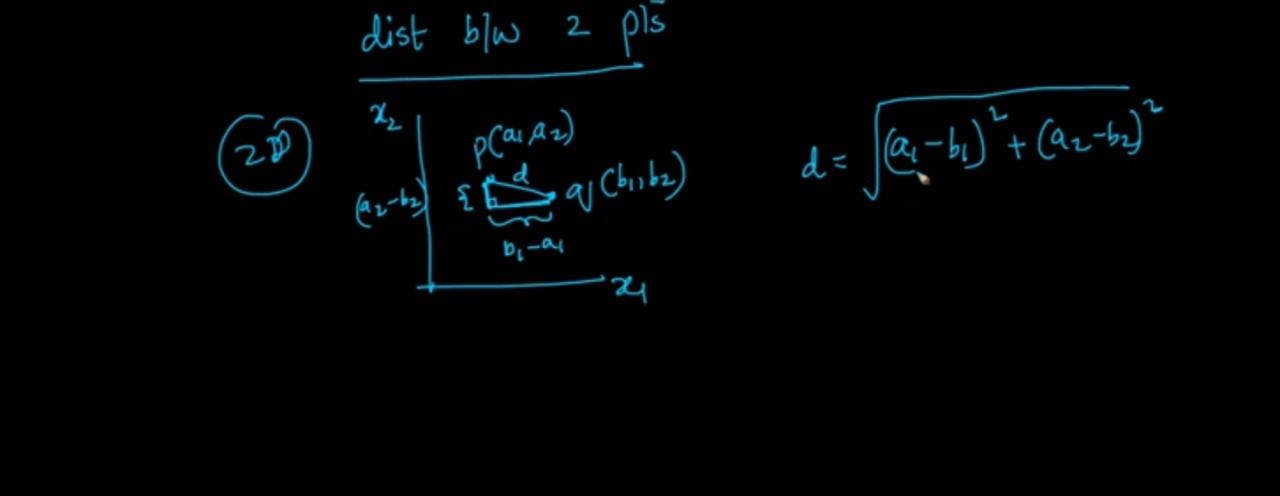
you can observe the length of the base of triangle=(b1-a1), and the similar length of the height of triangle=(a2-b2). Now apply Pythagoras theorem to obtain the distance between points p, q which is equal to
d=sqrt((a1-b1)^2 +(a2-b2)^2)
For 3D Space.
Let p and q be two points in 3D space. Such that p=(a1,a2,a3), q=(b1,b2,b3) so distance between p and q is represented by,
d=sqrt((a1-b1)^2 +(a2-b2)^2 + (a3-b3)^2)
For similarly two points p and q in N-D space p=(a1,a2,a3,....an),
q=(b1,b2,b3.....bn). And the distance between p and q is given by,
d= sqrt( i=1 to n sigma(ai-bi)^2)
